今回はコサイン類似度のアルゴリズム問題、令和5年度基本情報技術者試験 科目 B公開問題の問5を解いてみます。
問題


解き方
この問題を簡単にまとめると以下の公式部分をプログラム化する穴埋め問題となります。
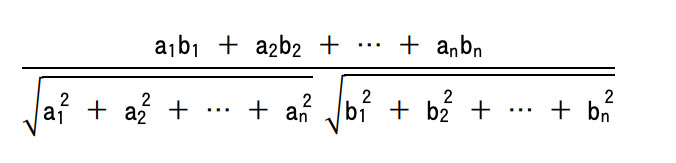
コサイン類似度やベクトルの知識はあれば良いですがなくても解けてしまいます。わかってしまうと見た目とは裏腹に割とシンプルなので見ていきましょう。
プログラムを分解して見ていく
まずはプログラムを分解して見ましょう。要は前述の公式をプログラムで計算するということをやっています。
分子と分母を表している部分
similarity ← numerator ÷ denominator
return similarity
この2行は最後の部分ですがこれでnumeratorが公式の分子、denominatorが公式の分母であることが予想できます。similarityは解ですね。
ちなみに英単語として
similarity:相似
numerator:分子
denominator:分母
なので英単語がわかればより明確になりますね。
分子を表している部分
for (i を 1 から vector1の要素数 まで 1 ずつ増やす)
numerator ← numerator + a
endfor
aの部分は選択肢から選ぶ空欄になりますが式を見ると分子部分の
a1b1 + a2b2 + … + anbn
が当てはまりそうなことが予想できますね。
そしてaの選択肢は以下になっています。
(vector1[i] × vector2[i])の正の平方根
vector1[i] × vector2[i]
vector1[i]の2乗
この中で式を確認すると2乗している部分がないのでまずはvector1[i]の2乗が選択肢から外れることはわかると思います。
次に問題や公式を確認しても「正の平方根」に該当しそうな部分もないためこれも選択肢から外れることがわかります。
分母を表している部分
for (i を 1 から vector1の要素数 まで 1 ずつ増やす)
temp ← temp + vector1[i]の2乗
endfor
denominator ← tempの正の平方根
temp ← 0
for (i を 1 から vector2の要素数 まで 1 ずつ増やす)
temp ← temp + vector2[i]の2乗
endfor
denominator ← b
上記が分母を表している部分になります。分母はさらに2つに分けられますので分けて考えて見ましょう。
for (i を 1 から vector1の要素数 まで 1 ずつ増やす)
temp ← temp + vector1[i]の2乗
endfor
denominator ← tempの正の平方根
temp ← 0
この部分でルートaの部分を表しています。tempという変数は次のルートbのところでも使いまわしているので初期化の意味で0を代入しています。
for (i を 1 から vector2の要素数 まで 1 ずつ増やす)
temp ← temp + vector2[i]の2乗
endfor
denominator ← b
そしてこちらでルートbの部分を表しています。また空欄bもここに含まれていますね。空欄の選択肢は以下になります。
denominator × (tempの正の平方根)
denominator + (tempの正の平方根)
tempの正の平方根
最初に確認したようにdenominatorという変数には分母全体が入ります。ルートaの部分のfor文でルートaの内容がdenominatorに格納された状態でルートbの最後の処理でdenominatorに何を代入するか問われている形ですね。
これを式に照らし合わせるとdenominator × (tempの正の平方根)が当てはまります。ここでのdenominatorにはルートaの部分の計算結果が入っており、 (tempの正の平方根)の部分にはルートbの計算結果が入っている形になります。
コメントを残す