ケタの重みとは

実は皆さん普段からケタの重みを使っています。
ケタを数える時、イチ、ジュウ、ヒャク、セン、マンと数えていますよね。
あれ実は「10進数のケタの重み」です。

より数学的に定義すると
n進数でケタが上がる時の値（10進数で表された値）のことです。

2進数で考えてみましょう。2進数で1から8まで（10進数での値）を表現すると次のようになります。

1, 10, 11, 100, 101, 110, 111, 1000

ここで桁が上がるタイミングだけ抜き出してみます。

2進数で桁が上がる数値 ｜1, 10, 100, 1000

10進数で↑を表した数値 ｜1, 2, 4, 8

２進数で桁が上がるタイミングの数値だけ書き出して

１０進数で書き直したものが２進数が持つ書く桁の重みと呼ばれるものになります。

つまり

2進数の重みは

1, 2, 4, 8

10進数の重みは

1, 10, 100, 1000

8進数の重みは

1, 8, 64, 512

16進数の重みは

1, 16, 256, 4096

となります。

重みを導き出す

重みを出す方程式は以下のようになります。

例えば2進数の重み(桁ごと)を出すには以下のように計算します。
（5^3は5の3乗という意味で5x5x5＝25のことです。またこの時の3は指数と呼ばれます。）

2^0 = 1（n（基数）の桁-1乗 = 1桁目の重み）

2^1 = 2 （n（基数）の桁-2乗 = 2桁目の重み）

2^2 = 4 （n（基数）の桁-3乗 = 3桁目の重み）

このやり方は基数が変わって８進数や10進数になっても変わりません。

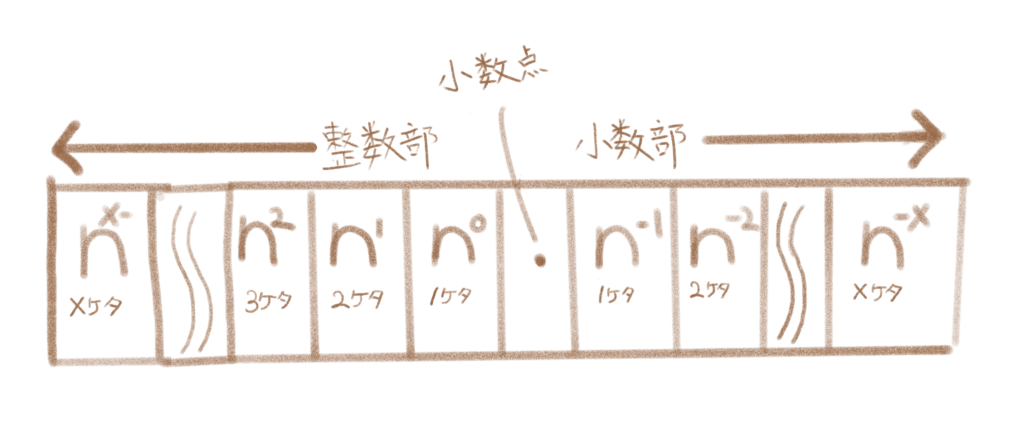
よく使う重み表

基数	n^3四桁	n^2三桁	n^1二桁	n^0一桁	小数点	n^-1一桁	n^-2二桁	n^-3三桁
2	8	4	2	1		0.5	0.25	0.125
8	512	64	8	1		0.125	0.015625	0.001953125
10	1000	100	10	1		0.1	0.01	0.001
16	4096	256	16	1		0.0625	0.00390625	0.000244140625

注意点

基数変換の時に重みを使う場面があります。
その際、2進数の重みを2,4,8と1を飛ばしてしまう勘違いがたまにあります。

重みは1から始まる

このことを何か覚えやすいイメージなどに変えて
自分なりに記憶しておくと良いでしょう。

私はイチローが重すぎるダンベルを持っているイメージを記憶として使っています。

指数について

指数の計算で少し特徴的なものも最後に挙げておきます。
例えば2^0、16^0、200^0これらは全て1を表します。

また指数がマイナスの値になることもあります。その際は以下のように計算します。