漸化式

漸化式とは最も簡単に説明すると数列の法則を表す表現方法です。基本情報技術者試験科目bで組み合わせの問題の際に使いましたので改めてまとめてみたいと思います。

前提知識

漸化式を知る前に以下の単語を理解しておきましょう。

数列

数字が特定の順番で複数並んでいるものが数列です。例えば「２、４、６、８・・・」は偶数の数列ですね。

項

数列に並んでいる各々の数字を項と呼びます。前述の偶数の数列では最初の項は２、2番目の項は４です。

一階線形漸化式

最もシンプルな漸化式です。例えば次の式を例に見てみましょう。

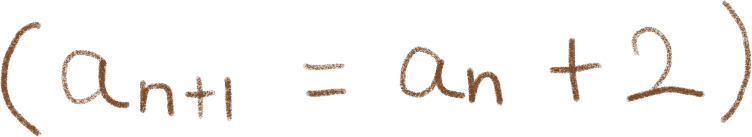
この式は前の項に２をプラスし続けて数列を作る漸化式になります。
式のaは数列の各項の値を表します。nは数列の何番目かということを表しています。

ではa1＝５として上記式をもとに計算をしてみましょう。

a2 = a1 + 2 = 5 + 2 = 7
a3 = a2 + 2 = 7 + 2 = 9
a4 = a3 + 2 = 9 + 2 = 11

5,7,9,11という数列aが出来上がりました。

高階漸化式

一階線形漸化式が直前の項に基づいて計算されるものだったのに対して、高階漸化式は直前の項に限らず複数の前の項に基づいて計算されるものです。代表的なものとしてフィボナッチ数列（各項が直前2つの項の和になる）があります。

フィボナッチ数列の例
0, 1, 1, 2, 3, 5, 8, 13…

まとめ

漸化式は数学の概念ですが知っていると何かと便利なようです。基本情報技術者試験でも組み合わせの問題で使えましたので知っておいて損はない知識のように思います。