集合｜基礎理論｜離散数学

基本情報技術者平成29年春期 午前問1の問題を解いてみます。過去問をやっていると割と見かける問題です。

問題

集合A，B，Cを使った等式のうち，集合A，B，Cの内容によらず常に成立する等式はどれか。ここで，∪は和集合，∩は積集合を示す。

ア　(A∪B)∩(A∩C) ＝ B∩(A∪C)
イ　(A∪B)∩C ＝ (A∪C)∩(B∪C)
ウ　(A∩C)∪(B∩A) ＝ (A∩B)∪(B∩C)
エ　(A∩C)∪(B∩C) ＝ (A∪B)∩C

解き方として２パターンありますので簡単な方から見ていきましょう。

簡易解法｜分配の法則

これは数学の式でも同様の考えがありますね。

（A＋B）x C ＝ AC+BC
（１＋２）x３ ＝ ３＋６

これは論理式にも応用ができます。

A ∪ (B ∩ C) ＝ (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) ＝ (A ∩ B) ∪ (A ∩ C)

選択肢を改めて見るとエが当てはまりそうです。
(A∩C)∪(B∩C) ＝ (A∪B)∩C

試験では時間がないのでこの簡易解法を覚えておくほうが良いでしょう。

詳細解放｜ベン図

ベン図を書くと確実に理解することもできます。ここでは正解のエのパターンを書いてみます。

(A∩C)∪(B∩C) ＝ (A∪B)∩C

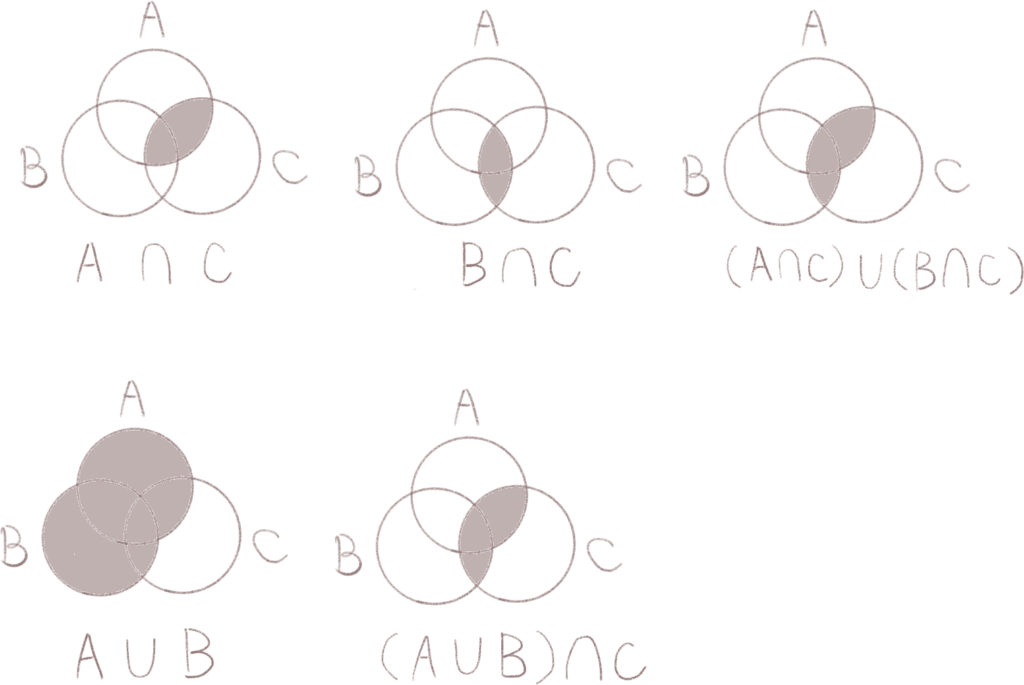
こうしてみると左辺と右辺の結果が合致していることが確認できますね。確実に理解したい場合や確認をしたい場合などはベン図に起こして見ると理解が進むと思います。