問題
100人の送受信者が共通鍵暗号方式で,それぞれ秘密に通信を行うときに必要な共通鍵の総数は幾つか。
- ア 200
- イ 4,950
- ウ 9,900
- エ 10,000
解き方
人数をnとした時、nが増えるごとに鍵がn-1増えます。わかりにくい場合は図を作成すると良いでしょう。
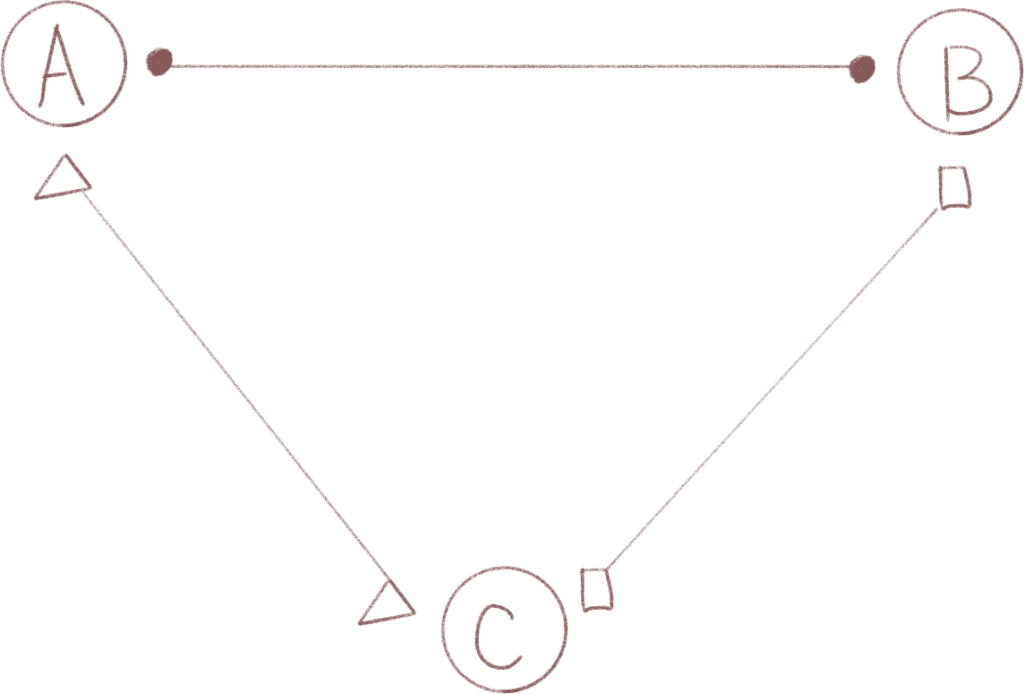
上記はA、B、Cという3人の例ですが丸と三角、四角がそれぞれ鍵になります。さらに図に人を追加して考えてみても人数が増えた場合を考えてもこのnが増えるごとに鍵がn-1増えるという法則は変わりそうにないことがわかります。
これは言い換えると相手の人数分の鍵を1人が持つとも言えますね。
確かに図を確認しても
Aは丸と三角
Bは丸と四角
Cは三角と四角
を鍵として所有しています。
ということは100人であれば一人が持つ鍵は99個です。
そこで以下のような公式が成り立ちます。
n(n-1)/2
これに100を当てはめると4950となり、イが正解となります。
※問題中の総数という部分については表現が曖昧だと思う方は正直少なくないと思いますが、共通鍵は通信元と通信先が同じものを使用、つまり1つの鍵で通信すると考えると腹落ちするのではないでしょうか?
コメントを残す