正規化

正規化とはデータベースにおいてデータの重複がなく、更新しても矛盾が生じない形に整理することをいいます。

正規化を理解するためにはまず正規化されていない非正規化の表を確認しましょう。

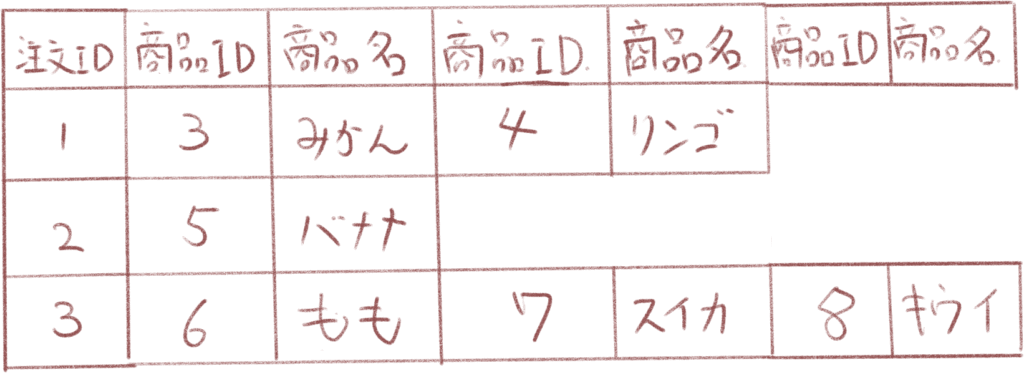
これは果物の注文記録を表にしたものですが注文ごとに種類が違うために同じ項目の列があり、また形も歪になっています。これを修正してみましょう。

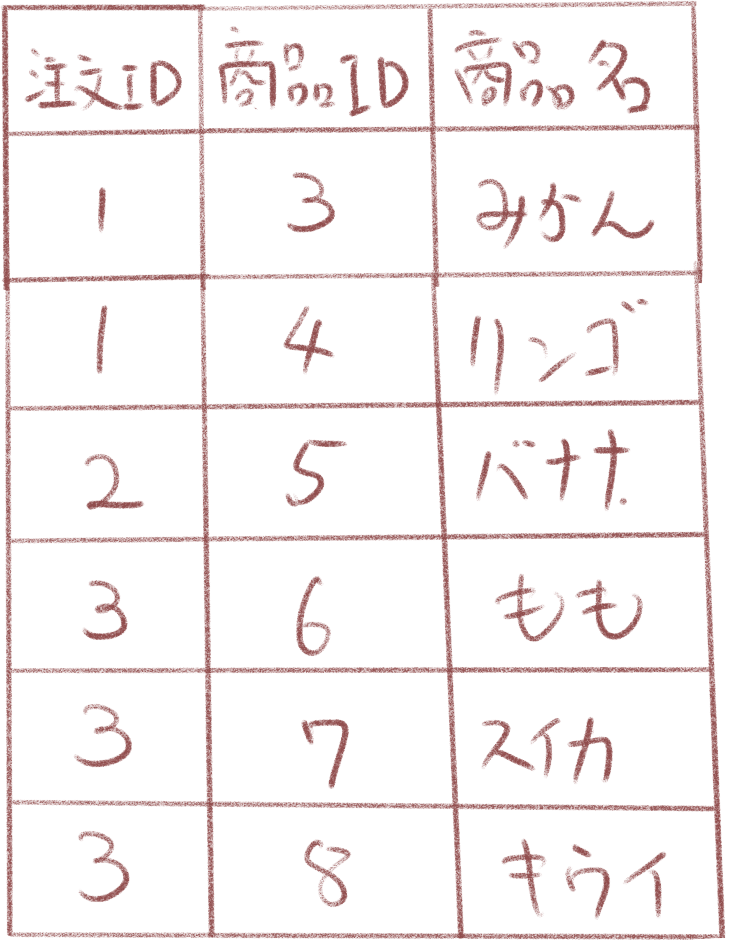
列の重複をなくしました。これを正規化（第一正規化）と呼びます。

関数従属

関数従属とはある属性（列）の値が決まることで別の属性（列）の値が一意に決まることを言います。下記の表では注文IDが決まると注文日が決まります。これは注文日は注文IDに関数従属していると言えます。

注文ID	注文日	備品番号	備品名	仕入れ先	単価	数量
10123	1/23	1	PC	A社	10万	2
10217	2/17	2	机	B社	3万	4
10308	3/8	3	椅子	C社	4万	7
10308	3/8	2	机	C社	3万	3

また関数従属には３つ種類があります。
・完全関数従属
・部分関数従属
・推移的関数従属

完全関数従属

完全関数従属とは『属性が主キーに関数従属すること』です。前述の表の注文日は注文IDが決まると一意に決まります。そして主キーは注文IDです。なので注文日は注文IDに完全関数従属しています。

ちなみに主キーが複合主キーであっても完全関数従属は成立します。

部分関数従属

部分関数従属とはまず『主キーが複合主キーであり、その一部に関数従属すること』を言います。以下の表を例に考えてみます。

注文ID	注文日	備品番号	備品名	仕入れ先	単価	数量
10123	1/23	1	PC	A社	10万	2
10217	2/17	2	机	B社	3万	4
10308	3/8	3	椅子	C社	4万	7
10308	3/8	2	机	C社	3万	3

この表で注文IDと備品番号が複合主キーで、備品名が備品番号によって一意に決まるとします。この時、備品名は備品番号に部分関数従属していると言えます。

推移的関数従属

推移的関数従属とは『ある属性（列）が主キー以外の属性（列）に関数従属すること』です。前述の備品注文表で考えてみると備品名が決まると単価が一意に決まるとします。この時、備品名は主キーではありません。よって単価は備品名に推移的関数従属していると言えます。

また以下のようにも説明できます。
列A、B 、Cがあったとして、A→B、B→Cが成り立てばA→Cも成り立つ。

この法則は数学用語で推移率とも呼ばれますが推移的関数従属においてもこういった説明がされます。
前述の備品注文表においては備品番号→備品名、備品名→単価という関係が成り立ちこれが推移的関数従属と言えます。

正規化の目的

関数従属が分かった上で正規化を再定義してみると、正規化の目的は表の中の関数従属から部分関数従属と推移的関数従属を分けて完全関数従属の表だけの組み合わせに分割することとも言えます。

それでは順番に確認していきます。

非正規形

非正規形は属性（列）に重複がある状態の表です。

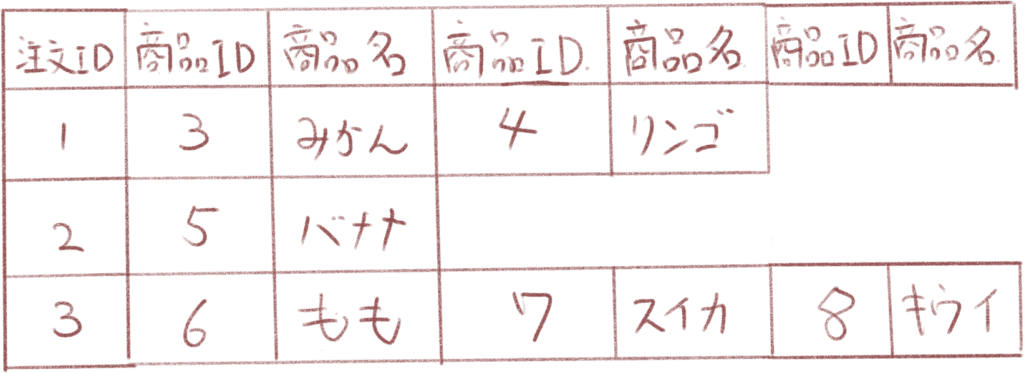
非正規系の表はリレーショナルデータベース（RDB,関係データベース）では使用できません。

第一正規形

第一正規形とは属性（列）の重複を解消した状態です。同じ表の中に新たな行を追加して属性（列）の重複を解消します。

第二正規形

第二正規形とは、部分関数属性がない状態にテーブル（表）を分割することを言います。

これは言い換えると複合主キーになっている表からそれぞれの主キーをベースにして表を作成するともいえます。

以下の表は部分関数従属しています。主キーが注文IDと備品番号の複合主キー、備品名は備品番号に部分関数従属しています。

注文ID	注文日	備品番号	備品名	仕入れ先	単価	数量
10123	1/23	1	PC	A社	10万	2
10217	2/17	2	机	B社	3万	4
10308	3/8	3	椅子	C社	4万	7
10308	3/8	2	机	B社	3万	3

この表を第二正規形にすると次のようになります。

注文ID	注文日
10123	1/23
10217	2/17
10308	3/8

備品番号	備品名	仕入れ先	単価
1	PC	A社	10万
2	机	B社	3万
3	椅子	C社	4万

注文ID	備品番号	数量
10123	1	2
10217	2	4
10308	3	7
10308	2	3

第二正規形が完了すると部分関数従属がなく完全関数従属のみになります。また注文表のID10308のように重複するレコードをまとめることもできます。備品の詳細部分が違ってくる部分のみ注文明細表で残しているので情報として削れている部分はない状態ですね。

ここまでで部分関数従属が取り除けました。ただ実は推移的関数従属は含まれています。しかし、第二正規形では推移的関数従属は含んでいて良いので覚えておきましょう。推移的関数従属は次の第三正規形で分離させます。

第三正規形

第三正規形とは、テーブルをさらに分割し推移的関数従属がない状態にすることです。第二正規形の最初の表、備品注文表を見てみましょう。ここでは備品名が決まると仕入れ先が決まります。これは推移的関数従属（主キー以外の列に従属している関係）にあたります。これを分離させてみます。

注文ID	注文日
10123	1/23
10217	2/17
10308	3/8

備品番号	備品名	単価
1	PC	10万
2	机	3万
3	椅子	4万

備品名	仕入れ先
PC	A社
机	B社
椅子	C社

注文ID	備品番号	数量
10123	1	2
10217	2	4
10308	3	7
10308	2	3

以上のように4つの表に分類できました。これで第３正規形まで完了しています。

このようにキーと従属する列を整理して細分化することでわかりやすく、また結合度を下げて管理ができるのでシステムが大規模になった時にも柔軟性、汎用性が増します。

第３正規形で複合主キーが含まれていても問題ない

以下の問題を見てみましょう。
令和5年度　12月実施分　修了認定に係る試験 問19

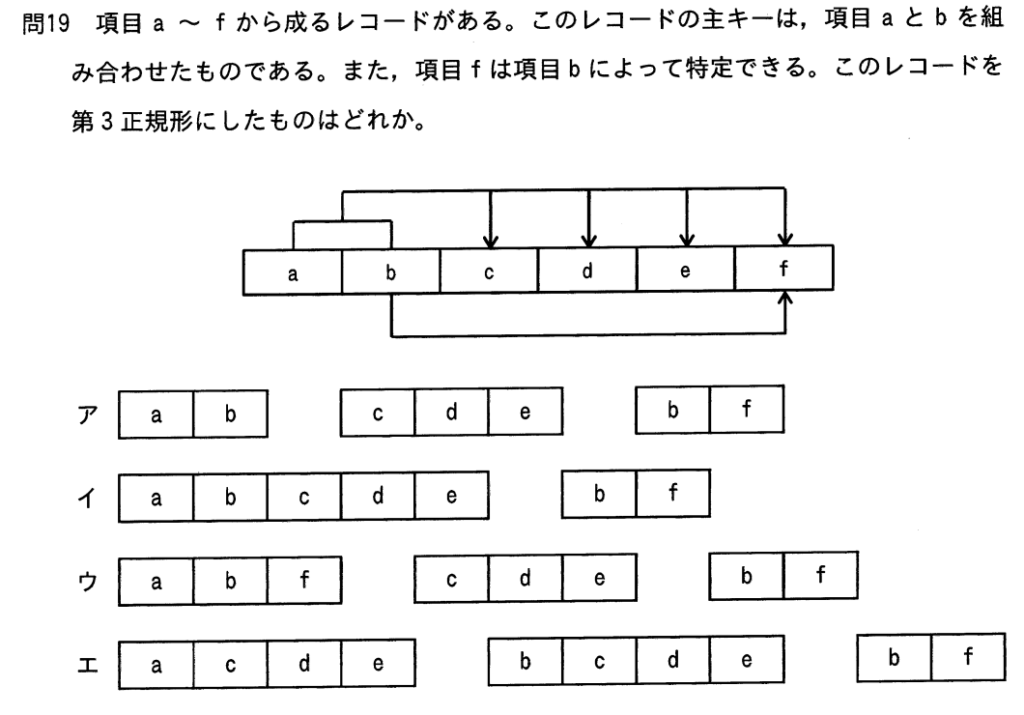
これ正解はイになります。イを確認するとabcdeという表が作成されています。これはabという複合主キーが入っていますが部分関数従属も推移的関数従属も解消された状態になっていますね。このように複合主キーは第3正規形で含まれていても問題ないので合わせて覚えておきましょう。