組み合わせの公式

_nC_r = n!/(r!(n-r)!)

これが組み合わせの公式になります。
これだけだと理解するのが難しいと思いますので問題を解きながら解説してみましょう。

問題

図の線上を，点Pから点Rを通って，点Qに至る最短経路は何通りあるか。

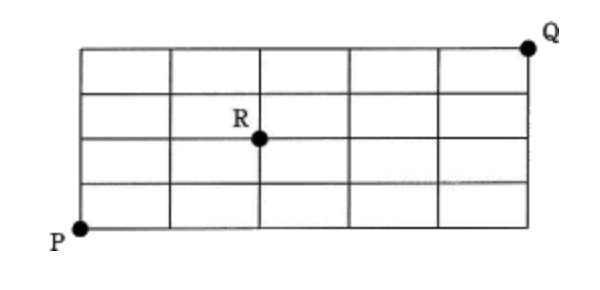
ア16　イ24　ウ32　エ60

解き方・考え方

まずはPからRまでの経路を考えてみます。
Pから４回移動するとRに最短経路で辿り着けます。

• ↑↑→→
• ↑→↑→
• ↑→→↑
• →→↑↑
• →↑→↑
• →↑↑→

この時上方向に２回、右方向に２回という原則があります。また上方向二回が決定すれば右方向も自ずと決定されます。これは4つの中から2つを選ぶ組み合わせと数と同じ数になります。

公式のおさらいと利用

_nC_r = n!/(r!(n-r)!)
このびっくりマークは階乗の意味でnから1までの数を全て掛けるということになります。そしてnは4回移動するので4、rはそのうちの2回が決まると組み合わせが決まるので2を代入します。すると以下のようになります。

₄C₂＝4x3x2x1/(2×1(2×1))=24/4=6

これで６通りということがわかりました。

同様にRからQを考えてみます

₅C₃ ＝5x4x3x2x1/3x2x1(2×1)=120/12=10

10通りであることがわかりました。

P→Q→Rの組み合わせはP→QとQ→Rの組み合わせを掛け算して求めます。すなわち

60通り

がこの問題の解になります。

この問題はほぼ数学なので公式を覚えて解くということを繰り返すのみだと思います。