論理シフトの例題練習

今回は論理シフトを利用して解く問題を例題として解いてみたいと思います。

この問題を見て論理シフトが思い浮かばないと難しくなるので、「ビットを入れ替える」や「256で割る」「256を掛ける」（←この256部分は2のべき乗であれば変化することもある。例えば8や512なども2のべき乗になります）などのキーワードを見たら論理シフトが使えそうだなという癖をつけたいところです。

問題の整理

まず仮の16ビットの2進数を設定（Xとして）して考えてみます。

10101111 00001111
（↑は10進数に直すと44815）

問題に「上位8ビットと下位」8ビットを入れ替えるとありますので入れ替えてみます。

00001111 10101111
（↑は10進数に直すと4015）

この状態を式で表したものを選択肢の中から選べという問題ですね。

論理シフト

ここで論理シフトの出番です。
桁をずらすと基数倍になったり奇数分の1になったりする法則があることを思い出しましょう。10から100は左に論理シフトして10倍になっていますし、10から1は右に論理シフトして10分の1になっています。2進数では10（2）から100（4）では2倍になっていますし10（2）から1（1）では2分の1です。

この法則を踏まえて式を眺めてみると256という数値から8ビットの論理シフトをやっていそうだということが予想できますので元の16ビットの2進数Xを上位8ビットと下位8ビットに分けて考えてみます。

Xの上位8ビットを抽出

まず上位８ビットを抽出することを考えると256で割るという方法があります。これは言い換えれば右へ8ビット論理シフトした値になります。

10101111 00001111 → 00000000 10101111（10進数に直すと175）

Xの上位8ビットが右に8ビットずれました。

Xの下位8ビットを抽出

次にXの下位8ビットを考えてみます。下位8ビットを抽出することを考えると元のXを256で割ったあまりで抽出できます。言葉だとわかりにくいので下記図を書いてみました。

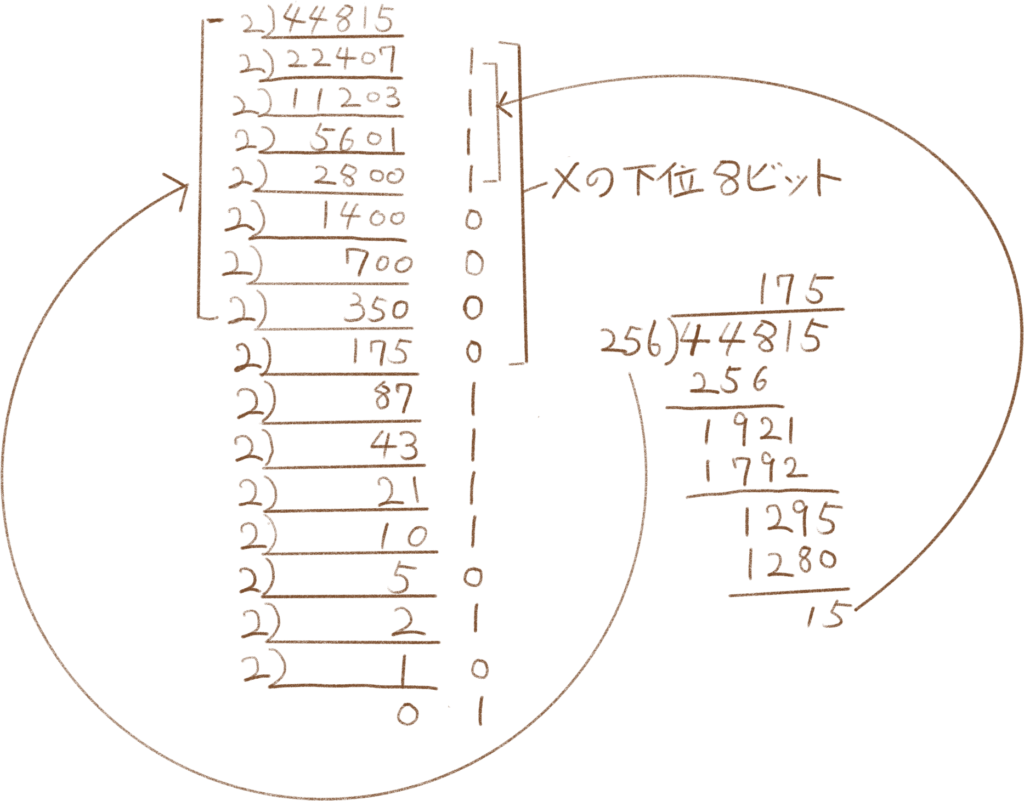
そして問題文にある「上位と下位を入れ替える」ということを実現するために左へ8ビット論理シフトします。これは256を掛けることでも同様に実現できます。以下では上記で抽出したXの下位8ビット（あまり15の1111）を左へ8ビットずらしています。

00001111 → 00001111 00000000

上位と下位を足して入れ替え完了

最後に以下を足し算します。

00000000 10101111 + 00001111 00000000 = 00001111 10101111

これで上位と下位を入れ替えた2進数が完成しました。

これまでの計算をおさらいしてみると
上位８ビットを抽出するため256で割る｜X div 256
下位８ビットを抽出するため256で割り余りをみる｜X mod 256
下位ビットを入れ替えるため256を掛けて左へ８ビット論理シフトする｜掛ける256

となりイが正解となります。